II. PROJECTIONS
PROJECTORS AND PROJECTIONS
As stated in the last lesson, this semester we will be making a pneumatic catapult. The video shows such a catapult in action:
What do you need to know first for all for this? Learning to understand technical drawings. You will make your parts from drawings of catapult parts which I will send you, from which you will then assemble the same catapult for yourself. After that, we will be able to conduct our joint experiments to study the aerodynamics of missile flight: that is, we will study how the conditions of a rocket's launch, its shape, weight, and design affect its flight range.
What does it mean: to understand a technical drawing? In simple terms, this means understanding what others are doing and being able to explain to someone else what you want to do. Depending on what you want to do, you will have to do this in different ways. You can even say that you have to use different languages for these technical communications.
Our catapult and rocket are mechanical products. Other examples of mechanical products are automobiles, trains, planes, buildings, tools, robots, shotguns, dishes, furniture. Engineers who make mechanical products are called mechanical engineers, or simply mechanics.
In addition to them, there are other engineers. For example, electronics and computer engineers. They do everything related to electricity in airplanes, trains, cars, computers and other mechanical devices as well as in electronic devices like computers, video cameras, phones etc.. Electronic engineers have their own language of technical communication. Over time, we will learn these basics.
In the meantime, we need to get acquainted with the language spoken by mechanical engineers. Its basis is technical drawing. Therefore, we will start with a technical drawing and ... geographical maps (Fig. 1). Look carefully at Figure 1. On the left side is a drawing of the implant, which is used to treat damaged joints in people. On the right, there is a map of the area.
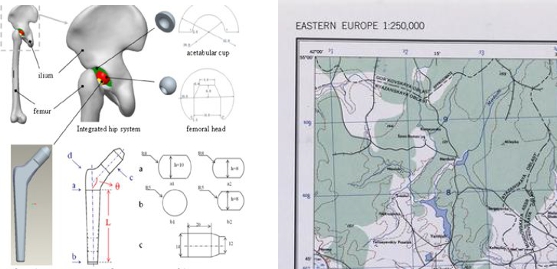
Fig. 1. Figure explaining the design of the implant and a map of the area
What do they have in common? Probably many of you will immediately notice two features common to them: 1) in both cases they are flat, i.e. they are two-dimensional drawings depict three-dimensional objects; and 2) the images on both the map and the technical drawing are not a simple drawing of the terrain or part. They use a number of conventions to transmit information about objects to us.
Conventionality One: Projection
What do we mean by projection?
Projection is the mapping of a three-dimensional object onto a plane. This plane is called the projection plane.
The simplest example of projections are the shadows of a 3-dimensional object on a wall. Watch the following videos for more information and to learn how to make your own projector, which you need for your homework:
1. Making a shadow theater projector: https://youtu.be/IwZ-dWM-3ls .
2. Work with the projector "shadow theater" : https://youtu.be/pLrR9jIiueA .
Video content:
- Transformations of three-dimensional objects into two-dimensional.
- Shadows and projections.
- Projection features in the projector "shadow theater".
3. Work with the projector "shadow theater"(continue): https://youtu.be/SJ6_DYz2Da0 .
Video content:
- Projections perspective and orthographic.
- Features of the conversion of three-dimensional and two-dimensional objects into two-dimensional.
- One-to-one and non-one-to-one transformations.
- Linear transformations.
4. How to make the simplest projection camera with a lens and projection glass: https://youtu.be/Eg_3xW3-GKU .
5. This video shows how to make a video projector using a mobile phone (just do not use your finger to apply glue, this is a very bad unsafe habit ): https://youtu.be/Tx4vPeL9y2g .
Let's summarize what we learned from these videos. With the help of our projectors, we transform a 3-dimensional object into a two-dimensional shadow. Schematically, such a transformation can be represented as a transformation of each point of a three-dimensional body to a point on the projection plane (see Fig. 2).
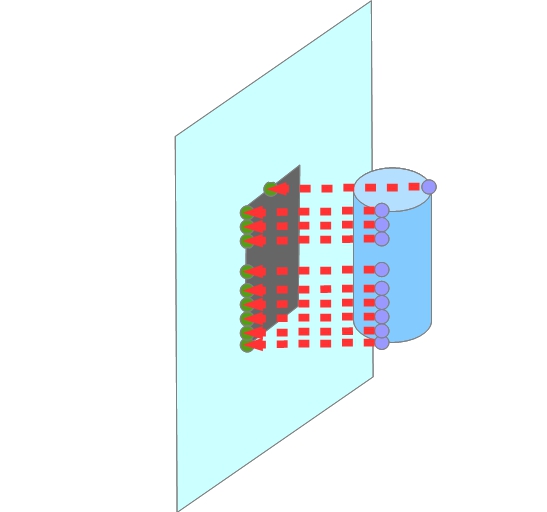
Fig. 2. Figure illustrating the transformation of points of a three-dimensional object onto a plane during projection
It can be seen from the figure that only for a part of the shadow outline can we indicate for one point only one original point of the projected body. And for most shadow points, several points of an object are projected at once into the same point. It turns out that each point of the cylinder corresponds to only one point of the shadow. But an arbitrary point of the shadow can correspond to several points of the cylinder at once. The following figure shows an example of such points (Fig. 3).
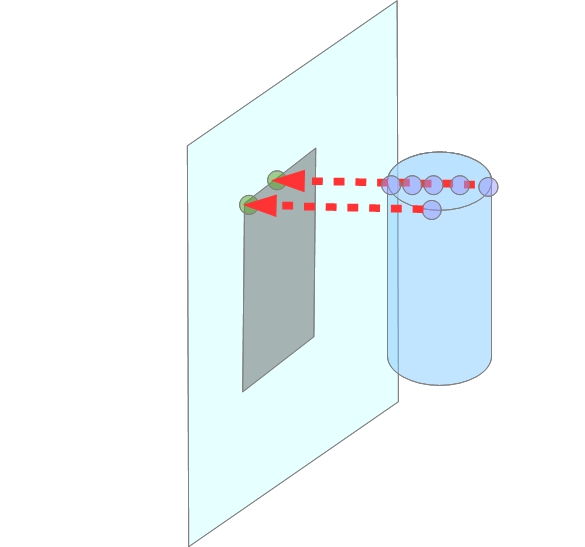
Fig. 3. An example of one-to-one (one cylinder point is projected to one shadow point) and many-to-one or non one-to-one transformation (several cylinder points is projected to one shadow point) of cylinder points on a plane is shown.
Therefore, the projection of a 3-dimensional object onto a two-dimensional, usually not one-to-one mapping, or else they say, is not a one-to-one transformation. In this case, this is not a one-to-one transformation of the cylinder into its shadow, a rectangle. Since with such a projection several points can be mapped onto one at a time, it cannot be said by the projection point which particular point was projected into it. In this case, it is obvious that part of the information about the original body is lost. Therefore, looking at a rectangular shadow, we will not be able to say exactly what shape the original 3D object was, because the same shadow can be obtained from a box.
As we have seen, projection can be carried out in various ways: using a light source (lamp, sun, flashlight), or a mechanical projector. For our projectors using a light source, the projection size may be larger or equal to the size of the projected object itself. Explain yourself why.
We can also use a transparent sheet of glass or plexiglass as a plane for projection. And with a felt-tip pen, circle the contours of the cylinder, as we see it (Fig. 4).
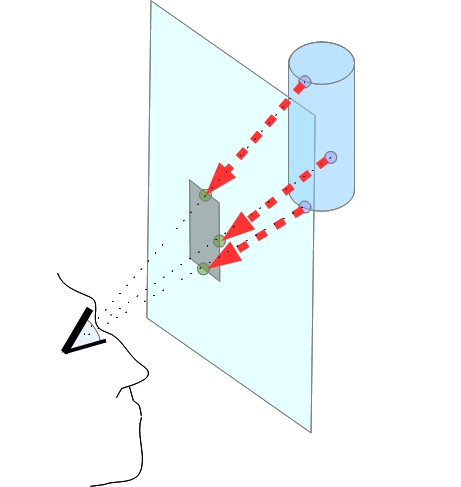
Fig. 4. Schematic representation of projection using a transparent screen.
That's just for sure it's hard to do. Try to make such a projection yourself and explain the difficulties of this method. What happens to dimensions with such a "visual projection"? Of course, changing the scale, i.e. by increasing or decreasing the resulting image, we can make the projection any size, including exactly the same as the original three-dimensional object. To facilitate "visual projection" in the 19th century, a pinhole camera was often used (https://youtu.be/IcNEfwNeZss ) but now we can use photography in addition to this.
Such a visual projection is also called a view. In contrast to the shadow, some other lines, faces, and features of the subject, which are not distinguishable in the case of a shadow, can be seen in the view. But the contours of the view and shadow coincide.