III. TECHNICAL DRAWINGS
The second convention: the reference point.
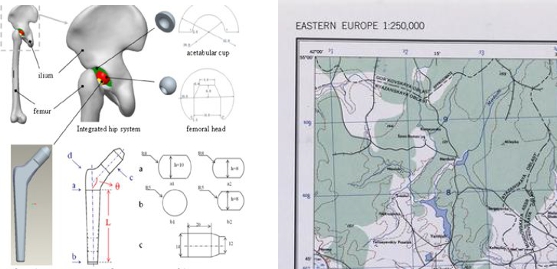
Fig. 1. Figure explaining the design of the implant and a map of the area
This convention is not entirely obvious. But there is always a reference point on all technical drawings and maps, since we always use landmarks to display the position of the body in space or on the plane. After all, the very concept of position in space implies a position relative to something. Such reference points can be special points on a piece of paper or a monitor screen, you yourself, objects on the ground, or parts of the object itself. When we use computer programs to create or view technical drawings, you will easily find such a point. From the reference point, the computer plots all sizes when it draws. In images on the computer screen, this point is called the origin. Its coordinates are zero. We will consider an example with eDrawings in this lesson.
When you draw yourself, though you don’t consciously do this. You often try to make the center of your drawing coincide with the center of the sheet. For you, that will be the main reference point, the starting point of your sketch.
In the usual technical drawing, dimensions are also always plotted. A well-drawn drawing should contain dimensions that are convenient for mechanics to read. Therefore, they must take into account the sequence in which the part will be manufactured. In addition, each part has its own functional features. For example, the size of the key must match the size of the keyhole. The side of the brick should be perpendicular to its other sides.
Therefore, the drawing always has a most important part. Either this part must be made especially carefully, or it must be made first. This part (plane, axis, or point) can be used as a reference part for other dimensions. It is called a datum.
Any map is created by measuring distances from selected reference points or landmarks. And when you go camping and use this map, you always use landmarks to plan your trip. Such landmarks may be the point where you start, or the point where you are heading, or some point of interest in a given area. Also on the map there is visible or is implied a coordinate grid with which you can determine the longitude and latitude of points on the terrain. They are measured in degrees. Why? Because any map is part of the surface of the earth’s globe. A terrestrial globe uses a spherical coordinate system, a 3-dimensional analogue of two-dimensional polar coordinates.
The origin of such a grid, its reference point, has a latitude of 0 degrees (the latitude of the Greenwich meridian, where the eponymous observatory is located, which from the 17th century was engaged in determining the coordinates of the terrain for mapping. The Zero standard itself was adopted in the 19th century) and 0 degrees of longitude (this is the longitude of the Earth's equator). A point with such coordinates is located in the Gulf of Guinea of the Atlantic Ocean.
The following videos explain this:
Polar coordinates
In drawings, we use the Cartesian (x, y) coordinates for 2D space, and (x, y, z) for 3D space. But there are other coordinate systems, for example, polar ones, that you used in your last homework. And then the coordinates of the point in 2-dimensional space are determined using the distance from the center of coordinates and the angle between the direction from the center of coordinates to the point and the X axis. The following video shows some examples of using polar coordinates. In this video, angles are measured in radians, while we usually measure angles in degrees. The ratio between radians and degrees is π = 180 degrees. The number π means approximately 3.14 radians:
https://www.youtube.com/watch?v=0xh32SzuUSU
One of the options for polar coordinates for 3D space is longitude and latitude on the globe. Only in this case, the radius is assumed to be constant equal to the average radius of the Earth. As already mentioned, such polar coordinates in 3-dimensional space are called spherical.
Convention three: scale
You won’t be able to use even the most carefully drawn drawing or map until you know how big your item is or how big the terrain shown on the map is. Therefore, it is customary to indicate real dimensions in the drawings. For maps, this is not the most convenient solution. Although it is used, for example, to indicate elevation on the ground. The easiest way is to specify the ratio between the size of the real object and the size of your drawing, sketch, or map. This ratio is called the scale. It shows the relationship between the unit of length in your drawing and the unit of length of a real object. For example, a 1:10 scale in the drawing says that 1 mm in your drawing corresponds to 10 mm in reality, i.e. your drawing is 10 times smaller than the real part. This method is used for both drawings and maps. For maps, it is often indicated graphically with a scale. The scale is usually located in the map legends and the scales there are of course completely different. For example, 1 cm: 1 km, i.e. 1 cm on the map is equal to 1 km on the ground.
These three videos will tell you a little more about the scale in drawings and maps:
And so we now know how to depict a three-dimensional object on a flat sheet of paper. But is this enough to explain the mechanics of what needs to be done? Alas, it is sometimes impossible to imagine a three-dimensional figure on one-dimensional projection. For example, we cannot say what is drawn on the side of the cube until we turn it with that side facing us. Therefore, in most cases it is necessary to use several projections of the object from different sides to get a complete picture. This is done on the implant drawing in Figure 1. For more complex parts, an even greater number of different projections is used. But how can we understand which figure corresponds to which projection? To avoid confusion, there is a rule for projection images. Figure 2 schematically shows the main projections. In the drawings, their origin is determined by the position relative to the main projection 1 (it is assumed that the viewer is located to the right of the cube, facing the side 1 and looks along the Y axis ) . The way projections are displayed in the United States is different from the conventions used in Europe. We will continue to adhere to the American system.
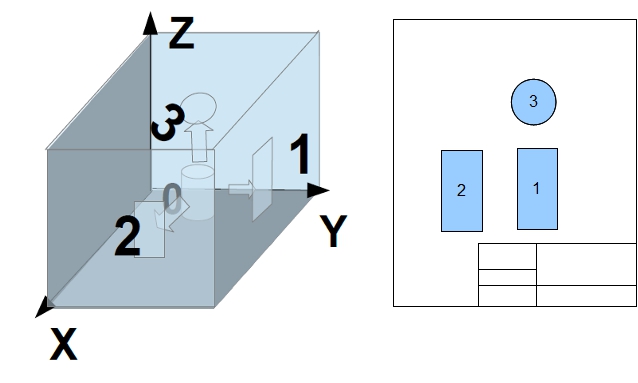
Fig.2. On the left is a schematic representation of the main projections, on the right is a schematic illustration of a technical drawing indicating the numbers of the projection. The main comments, such as the name of the part, scale, the name of the author of the drawing, are usually indicated in a special field limited by its additional frame. This field is shown in the lower right corner.
In addition to the above three, there are other standard projections for depicting a part from behind, from below, from the side opposite to number 2. An isometric projection is also often used to depict a general “quasi-volume” kind of part. An isometric projection is a projection along the direction in which the X, Y, and Z axes are visible as follows (Fig. 3):
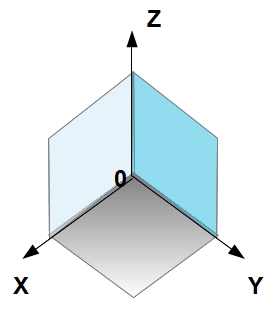
Fig.3 Isometric projection of a cube and coordinate system with origin
Here you can see animations explaining how to build standard projections in the American system (third angle projection)
Here you can learn how to draw the technical drawings manually:
Tolerances and annotations.
Have you ever looked inside the mechanical watch? If you have, then you saw a very complicated mechanical world of gears. These videos show how mechanical watches work and how they are made. You can even assemble your own watch should you be interested.
https://m.youtube.com/watch?v=9_QsCLYs2mY
https://m.youtube.com/watch?v=wfNOgWGME_c
https://m.youtube.com/watch?v=rDfde-nmtKg
You can find gears and gear transmissions in different mechanical mechanisms. Printers, automobiles, airplanes, trains, lathes, other mechanical tools and machines are using gears.
Now let’s practice making our own gear transmission. The following video explains you how to build a cycloidal gearbox. You should use these drawings of the gearbox parts (simply click on image with right mouse button, then use a "Save Image As ..." option to save images on your computer or download the homework zip file, then open files with these images and print them).
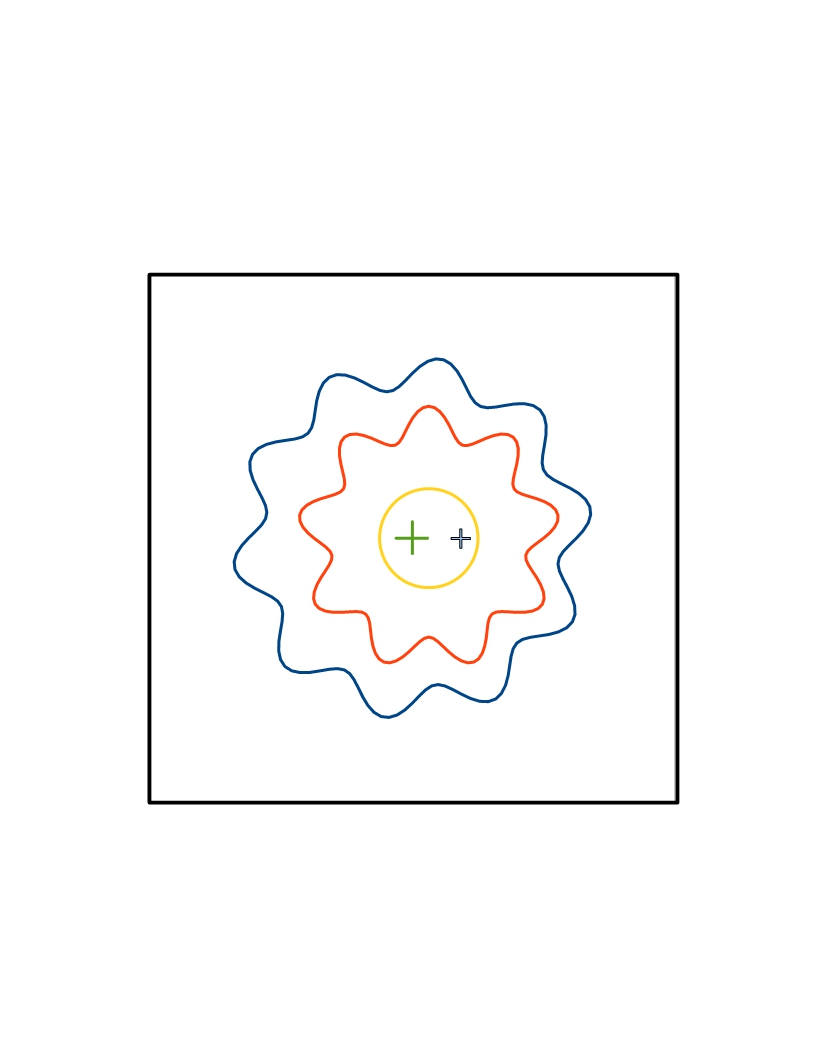
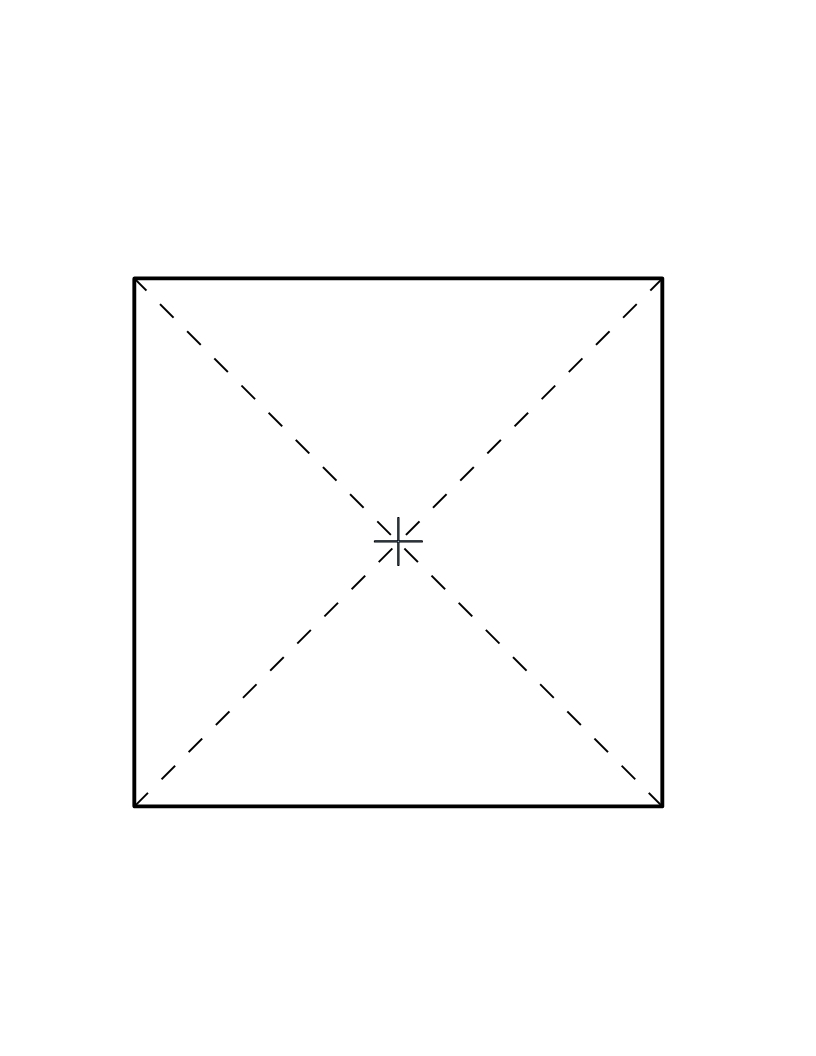
Try to build and investigate this gearbox yourself. You will learn that drawings should not just tell you about a shape and sizes of the mechanical device, which you are making. The good technical drawing should show you what are the most important parts of your device, how tight should be joints, how accurate dimensions. The reason is no one can make mechanical devices with absolutely exact dimensions. There are some variation always, and manufacturer should know how big variation are allowed: https://youtu.be/OGotSbNfNdE
The annotations and tolerances provide this additional information. For example, the requirement of free rotation of the disc in the gear can be specified as the diameter tolerances of the gear hole, 26.5mm+1mm, and the outside disc diameter, 26mm-1mm. This means, that gear hole can has diameter bigger than 26.5mm, but less than 27.5mm, while disc outer diameter has to be less than 26mm, but more than 25mm. This is a clearance fit. Should we use tolerance 26mm+/-1mm, it will tell you that the part dimension has to be bigger than 25mm, but less than 27mm. Usually, systems like “gear hole- disc” are called a shaft-hole system. There are special shaft-holes tolerance tables, which can help you to find right tolerances for free rotation or tight joint. Symbol ![]() inside the frame
inside the frame ![]() with an arrow pointing at a part means that the indicated part has to be positioned with accuracy of 0.5mm relative to the datum A. In other words, a distance measured between part and datum A should differ from the distance specified in drawing by less than 0.5mm (Fig. 4).
with an arrow pointing at a part means that the indicated part has to be positioned with accuracy of 0.5mm relative to the datum A. In other words, a distance measured between part and datum A should differ from the distance specified in drawing by less than 0.5mm (Fig. 4).
The millimeter, inch and microinch, as well as kilometer, meter, centimeter, nanometer and Angstrom are called dimension units. Dimensions in technical drawings are always in millimeters or inches(sometimes in microinches), and this is specified in the drawing annotation table or with text annotations. Therefore, dimensions are indicated by numbers and dimension units are usually omitted in the drawings of the parts.
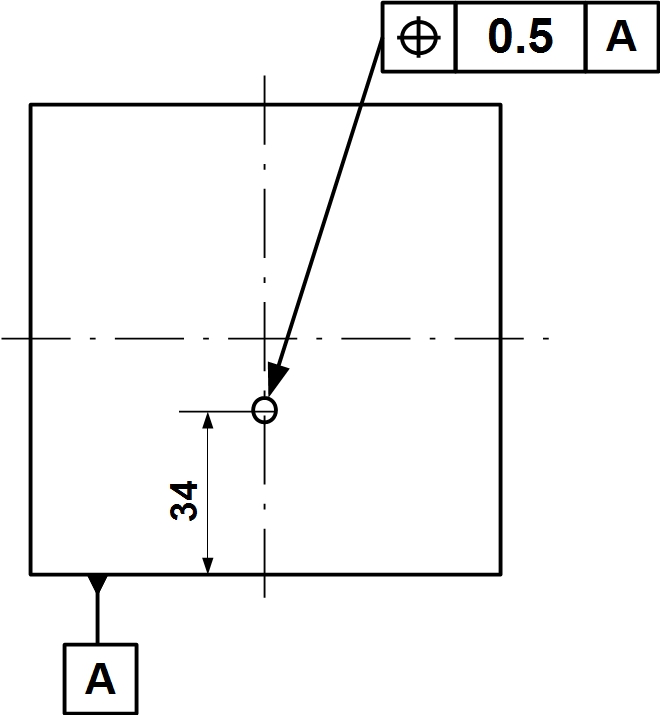
Fig. 4. Sketch of the square plate with hole that illustrates a geometrical tolerance designation in the technical drawings. Datum A is denoted as a flag (in the particular case it is an inverted flag). This tells us that the bottom side of the square plate is our reference side. The arrow of the boxed symbol points at the hole. This means that a position tolerance of 0.5mm is applied to the hole. Thus, the hole has to be located along the central line at a distance of 34mm from the datum side of the square with an accuracy of 0.5mm.
There are might be other symbols, which will specify requirements to the parallelism, concentricity, perpendicularity, cylindricity, flatness and etc. of the drawing parts. The following videos tell you about accuracy, precision and tolerance:
This video shows how tolerance can affect the properties of mechanical joints:
When you build your cycloidal gear, you should see that not just the diameters of hole and disc are important, but also how round they are. But how can you measure “roundness” (it is also called a cylindricity, because any hole or shaft has thickness)? The following video gives you a flavor of the real mechanical problems with measuring tolerances (video uses terms ID- internal diameter or hole diameter, and OD- outside diameter or shaft diameter):
The following video summarizes what we learned about the technical drawings so far. The video is good, but it may be difficult for you to watch it entirely in a single sitting. Therefore, pause when you are tired, take a rest and resume watching after. Do not be discouraged if you do not understand something. You can leave questions in your homework, and I will answer all of them:
eDrawings
We will now familiarize ourselves with the software that helps to make and view drawings. For now, we will use it to view CAD drawings and find various types (projections) of bodies instead of shadow theater. Download the freely available eDrawings program (free version):
https://www.solidworks.com/sw/support/eDrawings/e2_downloadcheck.htm
After you click on Download you will be offered a page on which you must confirm that you agree with the requirements for using the program. Then you download the file and open it.
To view a drawing file, you need to run eDrawings and then open the desired file with it. In this case, eDrawings may display a message that you need to install SOLIDWORKS Document Manager. You just need to click the button: “I will install later”.
Here's a video on eDrawings:
We use eDrawings to work with projections. Behavior of parallel lines in orthogonal projection: https://youtu.be/jo7xt5GLk_c
We work with projections in eDrwaings. Standard projections of technical drawings. Orthogonal and perspective projections: https://youtu.be/QwLOR_XI_S8
This video will briefly show how to use the main functions of eDrawings https://youtu.be/XPNS3b5q8rI
This is a tutorial on eDrawings (you will have a different version, but the button icons and their functions will be the same): https://www.youtube.com/watch?v=-yfIsHQGtts
Also download files that are attached to your homework . These are three-dimensional models of a cone, a cube and a ball. By rotating the models, you will get different views / projections onto the plane of the monitor screen (let's call it an imaginary piece of paper) from bodies rotated at different angles. Be careful. For example, the projection-shadow of a cone can have not only the shape of a circle and a triangle. If you conduct such an analysis of the figures, then it will be easy for you to answer correctly the questions of homework.
Please remember: you should zip the pdf file and then upload it, if you want to upload the pdf file in your homework reply.