Законы Ньютона и линейные преобразования.
Итак мы приступаем к изучению явлений гидростатики и гидродинамики. Что означают эти слова? Явления гидростатики- это явления которые происходят в покоящихся жидких средах. Соответственно гидродинамика описывает явления в текущих жидкостях. Эти явления очень важны, например, для строительства кораблей, самолетов, насосов, моторов, водопроводов, нефтепроводов, морских портов, гидро-, тепло- и атомных электростанций, химических реакторов. Т.е. везде, где применяются жидкости. Но оказывается эти же явления очень важны и для понимания явлений и в газовых средах, и в полупроводниковых приборах, и в радиосхемах.
ФИЗИЧЕСКИЕ ЯВЛЕНИЯ, ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ФИЗИЧЕСКИЕ МОДЕЛИ.
Как вы уже знаете, изучать физические явления- это значит строить модели этих явлений на языке математики. Явлением называется необычное, но обязательно воспроизводимое поведение одной из физических величин. Например тело начинает светиться, если приложить к нему электрическое напряжение. Или сопротивление электрическому току падает до нуля при охлаждении. Или крыло самолета начинает вибрировать при достижении определенной скорости полета. Или при росте температуры баллона с газом , давление газа тоже начинает расти.
Обычно явления обнаруживают экспериментально. Обнаружив явление, ученые первым делом пытаются убедиться, что это явление не случайное и воспроизводимое. Для этого надо понять, что приводит к возникновению этого явления и при каких условиях оно повторяется. Поэтому надо определить, какие физические величины и как влияют на это явление. Т. е. требуется определить взаимосвязь этих величин, а возможно и других величин изученных ранее, с наблюдаемым явлением. Этими физическими величинами могут быть время, вес тела, температура, скорость тела, яркость света, электрическое напряжение, и т. д.. Определив взаимосвязь величин и явления, мы поймем происхождение явления. Сможем ответить на вопросы, почему оно происходит, и при каких условиях оно происходит. Это позволит нам определить, случайно оно произошло или нет.
На языке математики, понять, как одна величина влияет на другую, значит найти математические преобразования, которые устанавливают соответствие между этими величинами, или, другими словами, преобразуют первую величину во вторую. Эти преобразования являются математическими моделями влияния одной физической величины на другую. В физике наиболее важные из таких преобразований, связывающих одни величины с другими, называются законами. Физические законы выражаются с помощью математики, но их правильность доказывается только экспериментальными измерениями.
Таким образом, объяснить наблюдаемое явление означает, во-первых, связать его известными или новыми законами с известными физическими величинами. Это и называется построить физическую модель явления. А во-вторых, используя полученные преобразования известных величин вычислить значения физических величин, при которых явление возникает, усиливается или пропадает, а результат проверить экспериментально. И если эксперимент подтверждает вычисления, то наша модель правильная.
ВЗАИМОДЕЙСТВИЕ ТЕЛ И ВТОРОЙ ЗАКОН НЬЮТОНА.
В качестве примера можно рассмотреть явление механики, когда на тело действует другое (например толкает его), и тело меняет свою скорость, ускоряется или тормозится. При этом, чем больше масса тела, тем меньше его ускорение/торможение. Как вы догадались, это действие называется силой. Чтобы понять, что такое сила, надо понять её свойства, как её обнаружить и измерить. В описании явления сказано, что оно связано с массой и ускорением тела. Ускорение говорит нам, как быстро изменяется скорость тела. В свою очередь скорость показывает, как быстро тело меняет своя положение в пространстве. Положение тела определяется по его координатам в выбранной системе отсчета.
Другая важная физическая величина для взаимодействия тел- это масса тел. Масса тела характеризует его инерционность. Инерционностью мы называем стремление тел сохранять свою скорость неизменной. Например, если тело покоится то, чтобы его сдвинуть, надо приложить силу. А если его не трогать, то оно так и будет покоиться.
Из описания явления следует, что сила прямо пропорциональна массе тела и ускорению тела, которое оно получило в результате действия силы на это тело. Это экспериментально обнаруженное правило называется вторым законом Ньютона.
ДЕЙСТВИЕ РАВНО ПРОТИВОДЕЙСТВИЮ ИЛИ ТРЕТИЙ ЗАКОН НЬЮТОНА.
Теперь мы знаем, как определить силу с которой одно тело действует на другое. Но вот интересно, у нас же два тела. Раз первое тело действует на второе, значит, в свою очередь, второе тело должно действовать на первое. Попробуйте толкните стену, и вы почувствуете, что она толкнула вас. Существует много опытов подтверждающих, что если два тела взаимодействуют друг с другом, то они действуют друг на друга с одинаковыми, но противоположно направленными силами. Фильм https://youtu.be/uV43M_NFASA показывает часть из них. Сокращенно, новое явление называют «действие равно противодействию». Это еще одно явление важное для понимания свойств силы. Оно называется третий закон Ньютона.
ИНЕРЦИОННЫЕ И НЕИНЕРЦИОННЫЕ СИСТЕМЫ ОТСЧЕТА.
Но всегда ли сила будет действовать в соответствии с третьим законом Ньютона? Вспомните, что произойдет с вами, если вы едете в автомобиле, а он резко затормозил. Сначала ваша скорость относительно автомобиля была ноль, ведь вы сидите в нем пристегнутые ремнем безопасности. Потом машина затормозила, и вас что-то толкнуло вперед. В результате вы ускорились, сдвинулись вперед, и только ремни не дали вам удариться о предметы спереди вас. Это что-то не машина. Ведь она затормозила, и тем самым толкала вас назад с помощью ремней безопасности, а не вперед. То что вас толкнуло, вообще не другое тело. Это что-то- вы сами. А точнее ваша собственная масса. Машина затормозила и ваша масса проявила себя в виде силы инерции. Вы ускорились и двинулись вперед. На вас подействовала сила. Об этом говорит второй закон Ньютона. Ведь согласно ему, если есть ускорение, то есть и сила. Да и вы сами это чувствуете. Но другого тела, которое толкнуло вас, нет. Явление взаимодействие тел не наблюдается, и третий закон Ньютона не работает, ведь сила инерции не вызвана другим телом.
Оказывается, законы будет работать только, если координаты тела, и соответственно его ускорение вычисляются относительно покоящегося или относительно равномерно и прямолинейно движущегося предмета. Но при ещё одной существенной оговорке: если на на этот предмет не действует никакая сила или действие всех сил равно нулю.
Например, относительно человека стоящего на тротуаре, вы ехали на машине с постоянной скоростью. Затем машина стала тормозить, и затормозила и вас. Для него, другое тело-машина толкнуло вас с помощью ремней безопасности в направлении, противоположном движению, и ваша скорость уменьшилась. Тут уже наши законы работают. И в этом случае пешеход никаких сил инерции не видит. Без ремней безопасности, вы бы просто продолжили двигаться с постоянной скоростью относительно пешехода и остановившейся машины. Ну и конечно, ударились бы о лобовое стекло затормозившего автомобиля.
А вот относительно другого пассажира, сидящего рядом с вами в тормозящей машине, это не так. Этот пассажир будет испытывать ту же самую силу инерции, что и вы. Относительно него сила инерции существует.
Это новое и тоже очень важное явление «влияние выбора системы отсчета», показывает, что наши законы выполняются только, если мы вычисляем ускорение в системе отсчета, движущейся прямолинейно с постоянной скоростью или покоящейся. Такие системы отсчета называются инерционными. Но опять повторю, при условии, если на рефересное тело, с которым связана система отсчета не действует никакая сила или действие всех сил равно нулю. Этот явление называется законом или принципом относительности Галилея.
Очевидно, что ключевым моментом для принципа Галилея является наличие таких тел, которые движутся равномерно и прямолинейно, или покоятся, если на них не действует никакая сила или действие всех сил равно нулю, и с которыми мы связываем инерционные системы отсчета. А есть ли такие тела? Существование таких тел доказывается опытным путем и является отдельным, очень важным явлением физики. Оно совсем не так просто, как может показаться на первый взгляд. Мы еще поговорим об этом отдельно.
Остается добавить, что перемещение, скорость, ускорение и сила — векторные величины. В этом задании мы пока будем всё применять только к одномерному случаю, т. е. движению вдоль прямой- оси Х. Поэтому знак вектора для простоты не указываем. О том, как это будет записываться с помощью векторов мы говорили в Задании 2 второго года обучения.
Перечисленные три явления настолько важны, что получили специальные названия: первый, второй и третий законы Ньютона, в честь Исаака Ньютона, который первым открыл их. Это видео https://www.youtube.com/watch?v=hTWZ8lMLGcg показывает еще несколько примеров из жизни на каждый из законов Ньютона.
ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ ДЛЯ НАШЕЙ МОДЕЛИ.
Три закона Ньютона, способы вычисления скорости, ускорения, особенности систем отсчета с системами координат- только все это вместе объясняет, что такое сила. И все это вместе будет нашей моделью механического взаимодействия тел.
Граф на Рис.1 показывает, как построена наша модель явления «тело действует на другое тело». Стрелочками показаны преобразования преобразующие одну или несколько величин в другую. Как хорошо видно из графа, в основе моделей явлений всегда лежат физические величины, которые мы измеряем непосредственно в эксперименте. Затем с помощью преобразований мы получаем из них остальные величины и выводим преобразования, которые описывают сами явления. Использование математических преобразований упрощает запись физических законов, позволяет проверять их с помощью вычислений. Но вы всегда должны помнить, что эти математические преобразования означают в реальном мире.
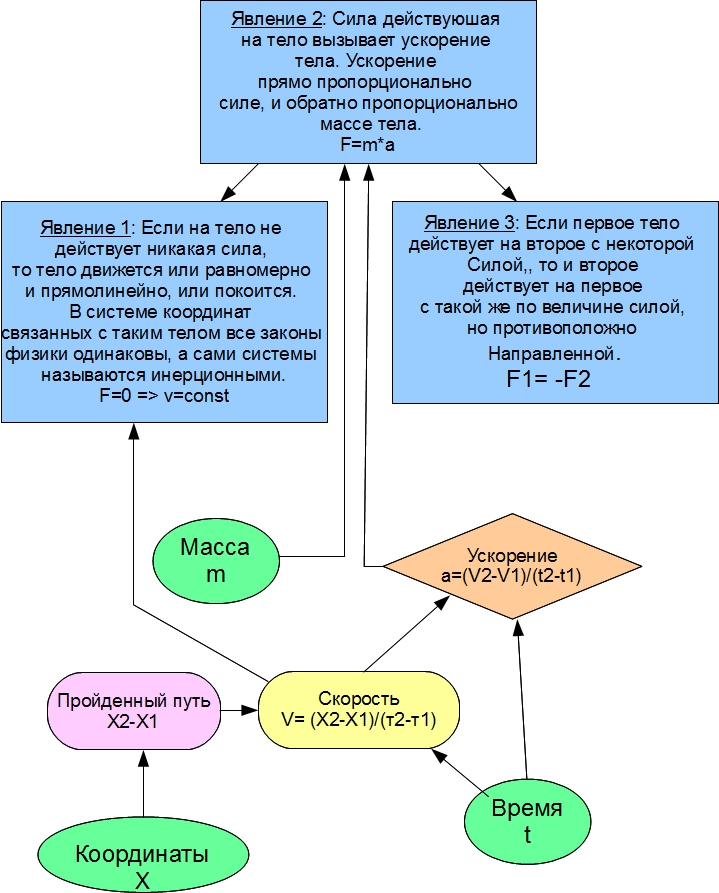
Рис.1. Схематичное изображение модели взаимодействия тел в механике. Как видите эта модель достаточно сложная. Она включает в себя три взаимосвязанных явления, и физические величины время, координаты и масса тела. Также она включает в себя величины пройденный путь, скорость и ускорение, которые получены с помощью преобразований из координат и времени. Также модель силы включает в себя три преобразования F=m*a; F1=-F2; и если F=0 то v=const, которые являются определением силы и её свойств. Конечно вы помните, что перемещение, скорость, ускорение и сила- векторные величины. Здесь же мы ограничились одномерным пространством- числовой осью Х, поэтому знаки векторов опускаем. Явление1 называется первый закон Ньютона; Явление 2-второй закон Ньютона; и Явление 3- третий закон Ньютона. Первый закон Ньютона гласит, что в инерциальных системах все законы физики одинаковы. В частности это означает, что в инерциальных системах отсчета мы имеем право пользоваться нашими преобразованиями для вычисления перемещения, скорости, ускорения и силы. В неинерциальных системах отсчета, преобразования для вычисления скорости, ускорения, и силы могут быть другими. Только рассматривая все это вместе, мы можем правильно объяснить, что такое сила, и как тела могут действовать друг на друга.
Напомню, система отсчета включает в себя точку отсчета и систему координат, в которой начало отсчета т. (0,0) совпадает с точкой отсчета. Вместо "точка отсчета" иногда используются термины "тело отсчета", "рефересное тело", "рефересная точка".
Добавим ещё, что силы могут быть разными. Существуют силы упругости, выталкивающая сила жидкости или выталкивающая сила Архимеда, электромагнитные, гравитационные и т. д. Для каждого типа сил существуют свои явления, которые дают возможность их вычислять, не прибегая ко второму закону Ньютона. Что позволяет использовать второй закон Ньютона не для нахождения силы, а для вычисления ускорения, скорости и положения тел. Т.е. в этом случае мы двигаемся не от физических величин к физическим явлениям, а в обратном направлении от физических явлений к физическим величинам.
Прежде, чем мы приступим к изучению известных моделей основных физических явлений и построению своих моделей гидродинамики, давайте вспомним основные понятия физики и математики, которые нам потребуются.
Сначала вспомним, что такое преобразование или функция.
ЧТО ТАКОЕ ПРЕОБРАЗОВАНИЕ.
Любое математическое преобразование преобразует одно множество точек в другое. Математические точки и числа могут использоваться для обозначения, чего угодно: цвета, веса, теплопроводности или температура. Всего, что может быть выражено числом. Но в математике у точки и числа нет ни температуры, ни цвета. Они не меряются ни килограммами, ни сантиметрами, ни секундами. Поэтому говорят, что в математике точки и числа безразмерные, т. е. у них нет размерности. Это просто точки и числа. Но когда мы используем точки и числа в физике, то мы наделяем их физическими свойствами: длиной, весом, температурой, временем и т. д. Мы придаем им размерность, и теперь их можно использовать для обозначения физических величин.
В математике вместо слова преобразование, часто используется слово функция. Множество точек которые функция преобразует, называется областью определению функции. Множество точек в которые они преобразуются- называется областью значений функции. Эти же математические понятия используются и в программировании.
Простейшая и наиболее часто употребляемая функция- это линейная функция, или линейное преобразование.
Например, если человек идет с постоянной скоростью, то длина пройденного им пути пропорциональна времени его путешествия. Функция здесь- это преобразование точек времени, в точки пути. То есть мы берем множество точек времени. Это область определения нашего преобразования. Эту область определения можно представить себе, как числовую прямую на которой точки- это точки времени: точка 0 секунд, точка 1 секунда, точка 2 секунды и т. д.(Рис.2) Пройденный путь, или область значений на языке математики, тоже можно представить себе в виде другой числовой прямой. Только на этой, второй, числовой прямой точками уже будут точки пути: точка 0 метров пройденного пути, точка 1 метр пройденного пути, точка 2 метра пройденного пути и т.д. Тогда например, точка О секунд отобразится в точку 0 метров, а точка 1 секунда в точку 3 метра, точка 2 секунды в точку 6метров, т. 3сек в т. 9м, и т.д. Если человек идет медленнее, то получится другое преобразование. Например, т.0 в т.0м, т.1сек в т.1м, т.2сек в т.2м, т.3сек в т.3м и т.д. При этом длина пройденного пути всегда будет прямо пропорциональна времени в пути. Это прямо пропорциональное преобразование и есть линейная функция.
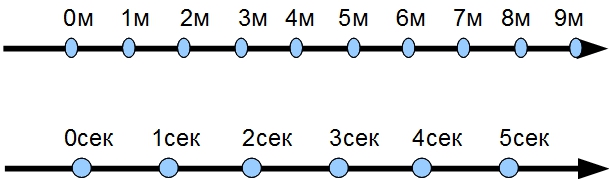
Рис.2. Две числовые прямые изображающие область определения- множество точек времени, и область значений-множество точек пройденного расстояния. Преобразование одного множества в другое, будет задавать конкретное соответствие между точками числовой прямой с размерностью времени и числовой прямой с размерностью расстояния. Например, преобразование т.0сек в т.0м, т.1сек в т.1м, т.2сек в т.2м, мы можем мысленно представить линиями соединяющими точку 0сек с точкой 0м; т.1сек с т.1м; т.2сек с т.2м; и т. д.
Другой пример: ортогональная проекция тела на плоскость. Скажем это может быть тень человека на вертикальную стену в лучах заходящего солнца. Тогда,чем больше человек, тем больше его тень (Рис.3а). А точнее во сколько раз больше человек, во столько раз больше размеры его тени. Т.е. размеры тени прямо пропорциональны размерам человека.
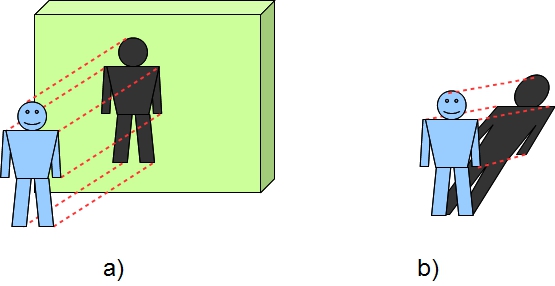
Рис. 3. Показывает параллельные проекции-тени человечка создаваемые солнечными лучами: а) частный случай параллельных проекций- ортогональная проекция человечка на вертикальную плоскость; b) солнечная тень человечка на горизонтальную плоскость.
Это может быть и параллельная проекция. Например солнечная тень человека на горизонтальную плоскость (Рис.3b). В этом случае размеры тени не будут равны размерам человека. Тень будет длиннее. Но все размеры удлинятся пропорционально, т. е. в одинаковое число раз. Скажем вся длина тени больше длины человека в два раза . Тогда у тени в два раза длиннее и ноги, и руки, и голова. Поэтому размеры тени все равно прямо пропорциональны размерам человека: во сколько раз больше один человек другого, во столько раз больше и размеры его тени.
КАК В МАТЕМАТИКЕ ЗАПИСЫВАЮТ/ПРЕДСТАВЛЯЮТ ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ.
Общий вид линейного преобразования математически (а точнее в математике говорят аналитически) может быть записан в виде:
Y=a*X +b,
где a и b некоторые константы; X обозначает точки области значений функции; а Y точки области значений функции. Пока их лучше всего представлять себя в виде точек числовых прямых, скажем OX и OY ( или упрощенно назовем их прямыми Х и Y). Если мы изобразим эти числовые прямые под углом 90 градусов, то получим ортогональную систему координат XY с осями Х и Y, с которой мы хорошо знакомы. В этой системе координат преобразование Y=a*X +b, задаст прямую линию, которая пересекает ось X в точке с координатой –b/a ; и ось Y в точке с координатой b (Рис. 3). Другими словами эта прямая проходит через точки (-b/a; 0) и (0, b). Такое представление линейной функции Y=a*X +b называется графическим. Значит графическим представлением линейной функции является прямая линия. На Рисунке 4 показаны случаи, когда a=3, b=0; a=1, b=0; и a=3, b=6.
Еще линейную функцию, как и любую функцию, можно представить в виде таблицы, в которой в одной колонке будут числа области определения Х, а в другой колонке -числа области значений Y (см. таблицы на Рис.4 для различных значений a и b). При этом мы подразумеваем, что каждому числу колонки Х соответствует только своё число колонки Y.
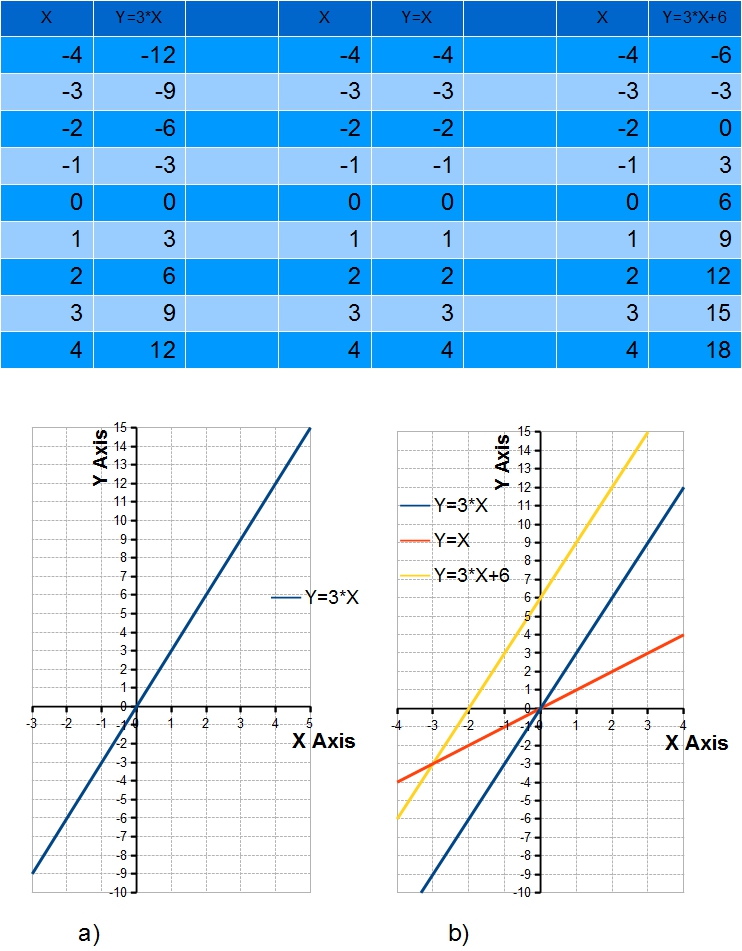
Рис.4. Показаны три способа записи преобразований: табличный, графический и аналитический для трех линейных преобразований Y=3*X ; Y=X ; и Y=3*X+6. На графике а) показано графическое представление линейного преобразования Y=3*X. На графике b) показаны разным цветом все три линейных преобразования.
Как ведите из Рисунка 4, задание функции или преобразование, всегда означает задание области определения, области значения и задания соответствия между отдельными точками области определения и отдельными точками области значения. В аналитическом случае это соответствие задается просто самим уравнением. В графическом- через координаты каждой точки графика. Ведь каждая точка графика задает пару чисел (x, y). Этим самым мы ставим каждому числу оси X в соответствие определенное графиком, число оси Y. В случае таблицы, каждому числу области определения X ставится в соответствие число области значений лежащее в той же самой строке. Как легко видеть каждая пара чисел (x,y) лежащая в одной и той же строке таблицы, является координатами соответствующей точки на графике функции, и может быть вычислена с помощью аналитического выражения функции. Поэтому все три способа могут быть использованы для записи функции.
Но у каждого из этих способов есть свои плюсы и минусы. Если есть только табличная запись, то по ней сложно сказать об особенностях функции. Но это именно то, что мы обычно измеряем в эксперименте. Графический наглядно показывает особенности функции. Например легко определить это линейная функция или нет. Но точность графического способа ограничена графическими возможностями, a они не высокие. Аналитический способ дает и представление о характере функции, и может обладать высокой точностью. К сожалению точная аналитическая запись возможна не всегда, а в случае сложных функций не так то просто увидеть особенности поведения функции при разных значениях переменных X.
Обычно в экспериментах, при записи измерений физических величин используют табличный способ. Для удобства работы, для облегчения анализа данных- часто используют графическое представление. Но для установления закономерностей, создания физических моделей используется именно аналитическая запись преобразований. И все законы физики, которые тоже устанавливают связь между разными физическими величинами, записаны этим способом.
Замечание. Таблица может быть повернута на 90 градусов. Тогда данные будут записаны не в столбцы, а в строки. А пары чисел связанных преобразованием будут в столбцах вместо строк.
Остановимся подробнее на понятиях точки в математике и физике.
ПОНЯТИЕ ТОЧКИ В МАТЕМАТИКЕ.
Мы встречаем математические точки в геометрии, в алгебре при обозначении точек числовой прямой, при определении преобразований. Точка в математике не только не имеет размерности, она еще и не имеет размера. Она бесконечно маленькая. Это означает, что в любой самой маленькой окрестности любой точки на плоскости, или на прямой, в пространстве или в объёме любой из известных вам геометрических фигур, таких как шар, пирамида, конус, цилиндр, параллелепипед, куб, всегда есть бесконечно много других точек.
Вспомним теперь некоторые понятия механики, которые нам пригодятся.
ПОНЯТИЕ МАТЕРИАЛЬНОЙ ТОЧКИ.
В физике используется понятие материальной точки. Материальная точка- это самая маленькая часть тела, какую мы можем измерить. Она не обязательно должна быть меньше атома. Все зависит от наших измерительных инструментов. По другому можно сказать, это зависит от точности наших измерений. Например, если у нас есть только миллиметровая линейка, то точку с размерами 1/10мм=0.1мм можно считать материальной точкой, поскольку мы уже не сможем отличить её от точки, например, с размером 1/100мм.=0.01мм. Но если мы будем работать с электронным микроскопом, то для нас материальной точкой может стать часть пространства с размером 1/100000000мм=1E-8мм =0.00000001мм. Только нам не всегда нужна очень большая точность. Точность наших измерений во многом определяется самими явлениями, которые мы измеряем. Для исследования большинства механических явлений и работы механических механизмов окружающих нас, достаточно точности измерений 1/100мм=0.01мм.
Материальная точка в физике поэтому имеет конечные размеры, и может обладать физическими свойствами данного тела. Например у неё может быть масса, температура, теплопроводность и т. д. Этим всем она отличается от математической точки. Но тем не менее, в наших моделях для её описания на языке математики, мы используем понятие математической точки, потому, что как сказали, с точностью наших измерений, для нас материальная точка- самый маленький объект из возможных. Что нам это дает? Это позволяет нам вводить и использовать координаты. Ведь мы можем указать только координаты отдельно взятой точки тела, а не тела вообще.
Всегда ли в физике мы можем заменять очень маленький объект материальной точкой? Нет не всегда. Например при описании свойств электрона, его лучше представлять в виде облака (правда очень маленького облака гораздо меньше 1мм), а не точки. Более подробно о подобных явлениях мы будем говорить в следующем году.
Вы уже использовали понятие материальная точка для понятия центра масс и центра тяжести тела, для описания точки приложения силы к телу, и для определения координат тела. Если вы подзабыли, как мы это делали, то посмотрите Занятие 1, вторая неделя по программе второго года обучения ; Занятие 1, третья неделя ; Занятие 2, первая неделя по программе второго года обучения ; Занятие 2, вторая неделя по программе второго года обучения
ПОНЯТИЕ КООРДИНАТ, СКОРОСТИ И УСКОРЕНИЯ.
Главная задача механики- это уметь предсказывать положения тела или его части в пространстве через заданное время. Например нам надо уметь предсказывать движение частей двигателя автомобиля в течении всех циклов его работы. Предсказывание на завтра положения туч и облаков на небе необходимо для правильного предсказания погоды. Нам важно знать куда долетит самолет, где пролетит комета, когда будут морские приливы и отливы. И так далее.
Для того чтобы предсказывать положение тела или его частей, нам необходимо уметь характеризовать положение тела в пространстве. В математике для этого используется понятие координат точки. Аналогично, в физике для этого вводится понятие материальной точки и ее координат. Затем любое тело можно представить, как множество материальных точек. Тогда измерив координаты каждой точки, можно определить положение тела и его перемещение в пространстве. Понятно это очень громоздкий способ, ведь тело содержит миллионы таких материальных точек. Поэтому существует более простой способ. У каждого тела есть центр масс. Это тоже материальная точка. Тогда произвольное движение тела можно описать в виде комбинации двух движений: плоско параллельного движения тела и вращения тела вокруг точки центра масс (плоско-параллельное движение- это движение, при котором все точки тела движутся одинаково. Поэтому они движутся так же, как точка центра масс).
Мы пока изучали только плоско-параллельное движение, т. е. движение без вращения тела и его частей. В этом случае достаточно приписать материальной точке центра масс , массу всего тела, а затем следить только за движением центра масс. Это означает, что в физических моделях, мы можем заменять тело на материальную точку- центр масс тела, с массой равной массе всего тела. Как находить центр масс, вы уже знаете.
Ещё раз напомню, что материальная точка - это логическое понятие, обозначающее маленький объем пространства или тела, который мы выделяем мысленно. В реальности таких точек нет. Тоже самое относится и к центру масс. Например, у бублика центр масс есть. Его можно найти экспериментально. Его можно вычислить и не прибегая к эксперименту. Но никакой реальной точки там нет. Как все прекрасно знают, там есть только «дырка от бублика». Тем не менее мы можем использовать понятие центра масс для описания и предсказания движения бублика, как говорили ранее. Например, можем заменить бублик его центром масс с массой бублика для предсказания положения бублика при его падении или скольжении по столу, если он конечно не вертится. И мы можем проверить наши предсказания экспериментально и убедиться, что наша механическая модель бублика, в которой есть центр масс, правильная. Вот такой интересный парадокс.
Другой интересный парадокс. Центр масс тел связан с понятием центра тяжести тел. Оба центра- материальные точки, и обычно это одна и та же материальная точка. Но во вращающихся телах, например в гироскопах, оказывается, что центр тяжести может находится вообще в любой точке оси вращения.
Всякое движение точки характеризуется изменением координат точки во времени. Значит нам надо уметь измерять координаты центра масс и время. Для измерения координат точки вводится система координат. Как вы уже знаете- это могут быть Декартовы (или ортогональные) координаты, полярные координаты (например полярные на плоскости, или сферические в пространстве- это координаты которыми пользуются радары), и цилиндрические координаты (Рис.5). Мы пока будем пользоваться только Декартовыми координатами.
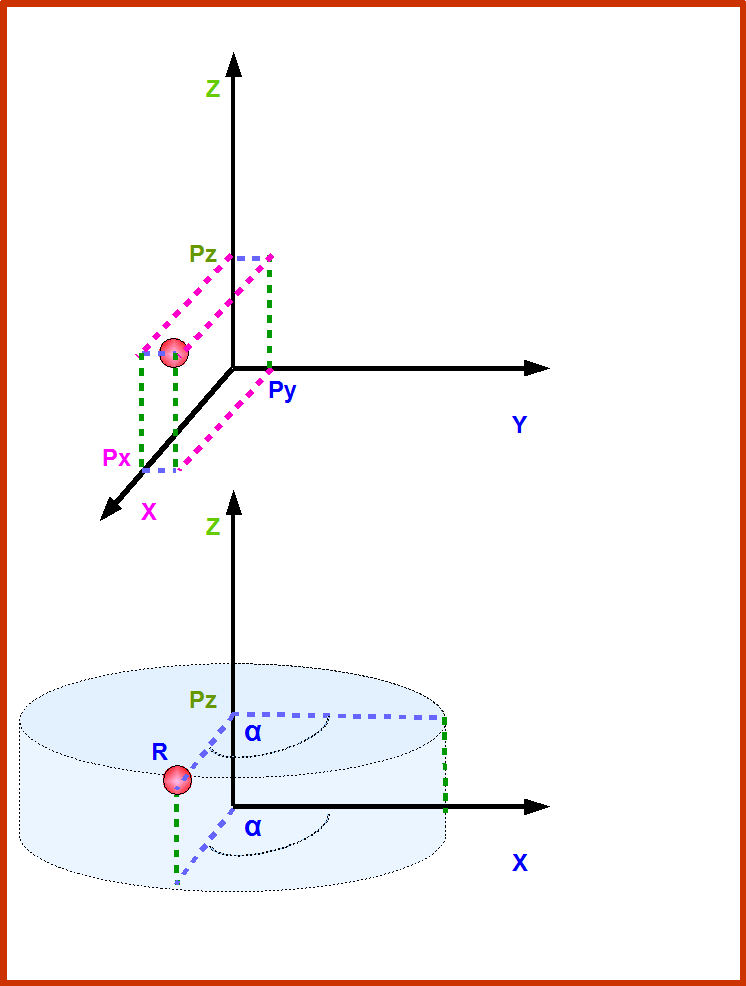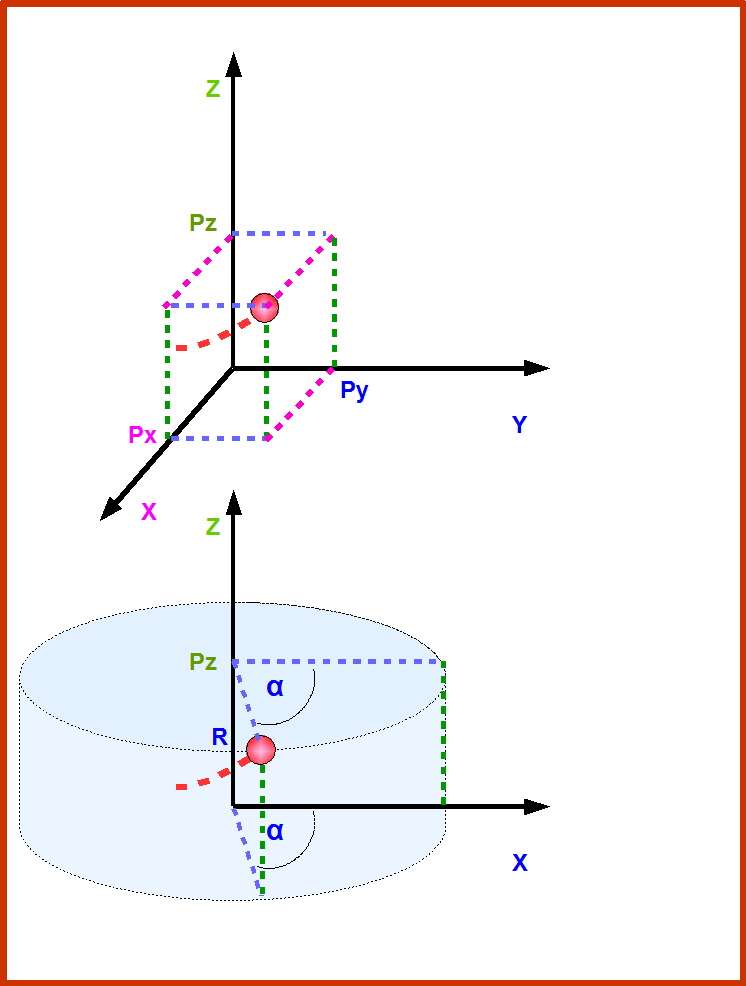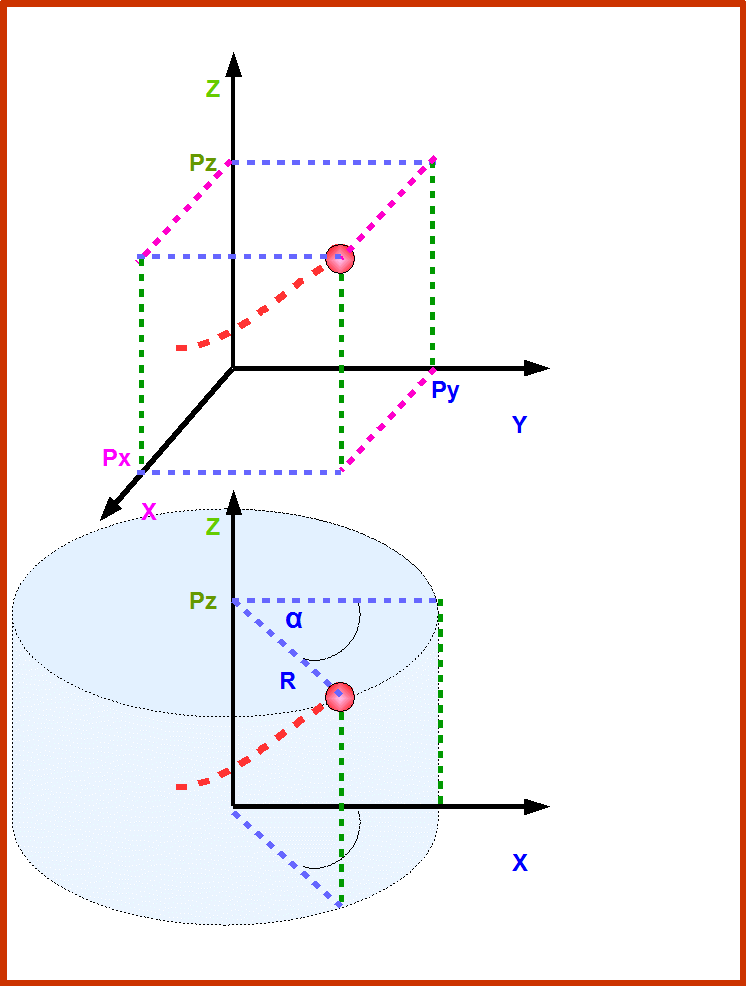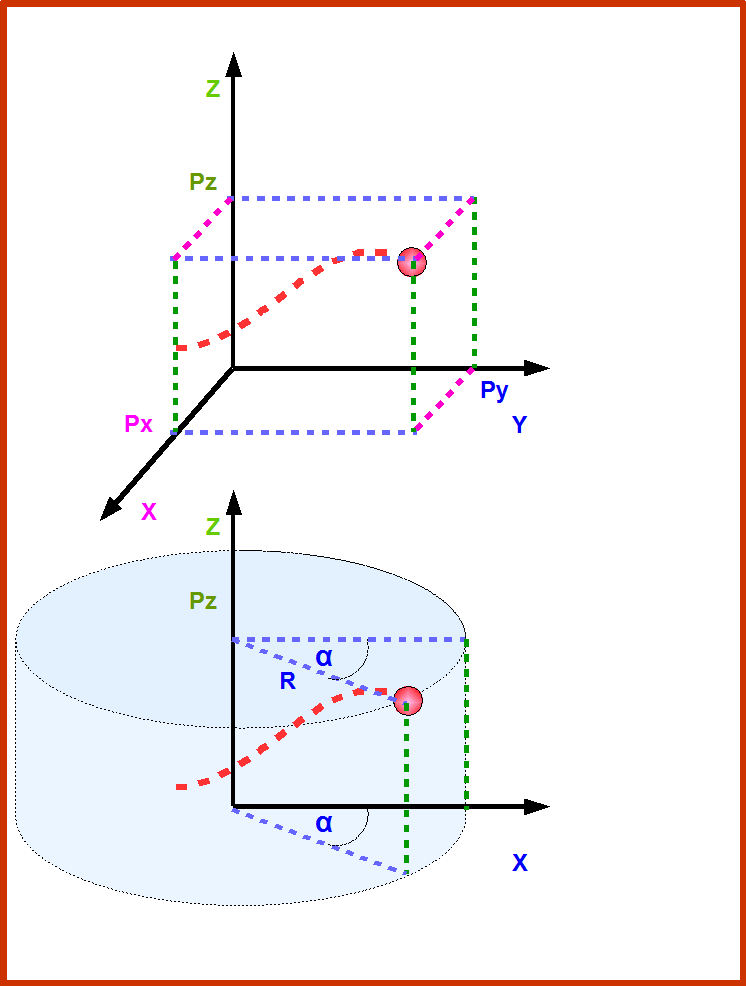
Рис.5. Показано как с помощью Декартовых и цилиндрических координат определяются координаты движущейся точки в трехмерном случае. Траектория точки показана красной штриховой линией. Поскольку это трехмерное пространство, то в каждый момент времени движущаяся точка имеет 3 независимых координаты. В Декартовых координатах- это тройка (Px, Py, Pz). В цилиндрических- это тройка (R, α, Pz). Чтобы определить Декартовы координаты, надо спроектировать точку на оси X, Y, и Z. Для этого можно нарисовать мысленно параллелепипед с ребрами лежащими на осях и с вершиной в точке. Чтобы определить координаты в цилиндрической системе, нам надо мысленно нарисовать цилиндр с осью лежащей на оси Z и основанием цилиндра проходящим через т.0 оси Z. Затем нам надо выбрать плоскость относительно которой мы будем измерять угол. В нашем случае-это плоскость XZ. Тогда тройка (R, α, Pz) означает: R- радиус цилиндра, α- угол между плоскостью проходящей через точку и плоскостью XZ взятой за нуль отсчета; Pz- высота цилиндра.
Чтобы ввести любые координаты, необходимо сначала выбрать точку относительно которой мы будем рассматривать движение нашего центра масс. Это точка начала отсчета или рефересная точка. Затем надо начало координат выбранной системы координат (в нашем случае Декартовой) поместить в эту точку. Поэтому любые координаты всегда относительны. Они всегда меряются относительно точки отсчета. Координаты точки отсчета всегда будут (0,0) в выбранной системе координат. Если мы перейдем в другую систему координат с другой рефересной точкой, то координаты точек изменятся.
Пока мы будем измерять координаты всегда в одной и той же координатной системе. Т.е. наша рефересная точка не меняется.
Итак мы умеем измерять координаты точек, и можем измерять время. Этого нам достаточно, чтобы измерить скорость движения точки. Пусть тело движется по прямой линии (Рис.6). Пусть в момент времени t1 положение центра масс телa было S1, а в момент времени t2 положение центра масс телa было S2. Тогда скорость движения центра масс:
v=(S2-S1)/(t2-t1).
Словами это можно сказать так: скорость- это изменение пройденного пути за промежуток времени делённое на этот промежуток времени.
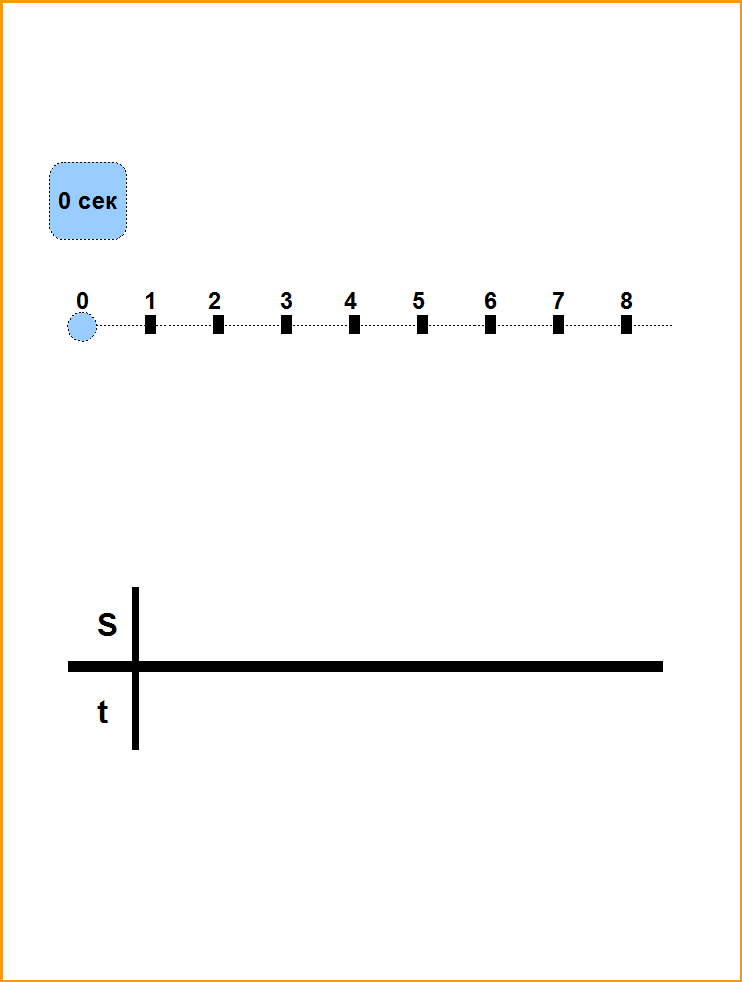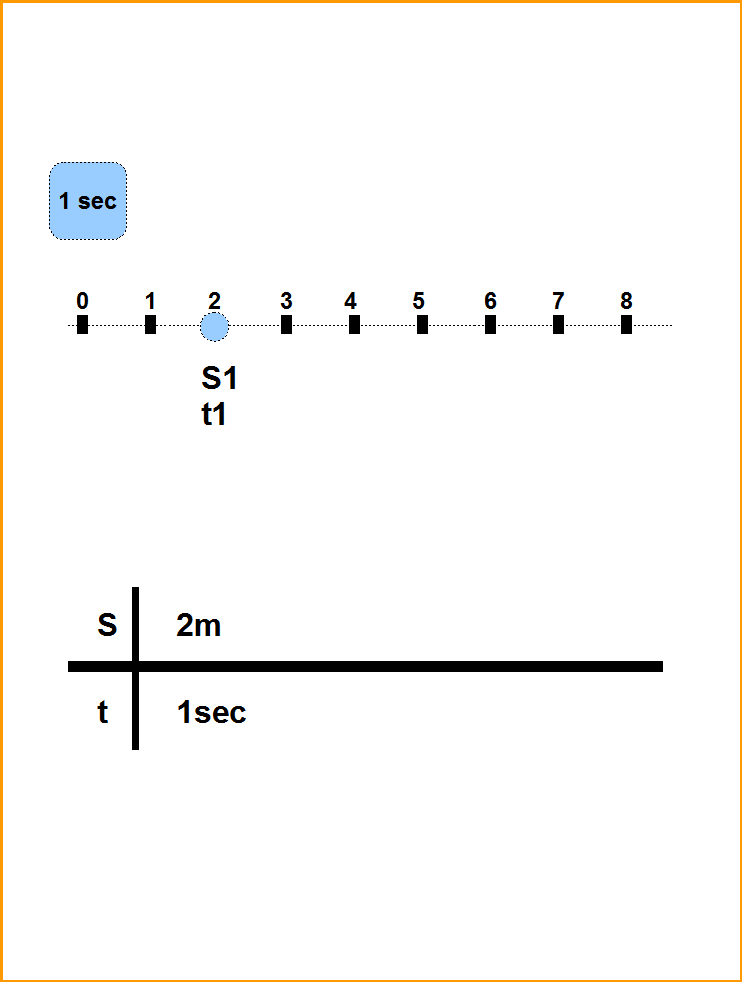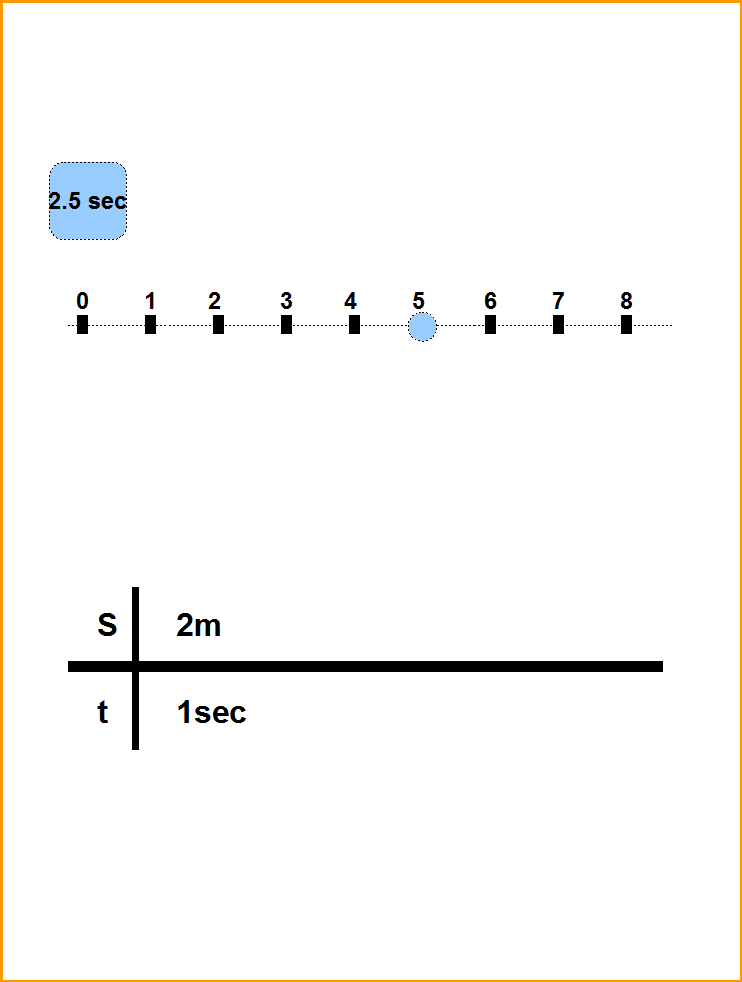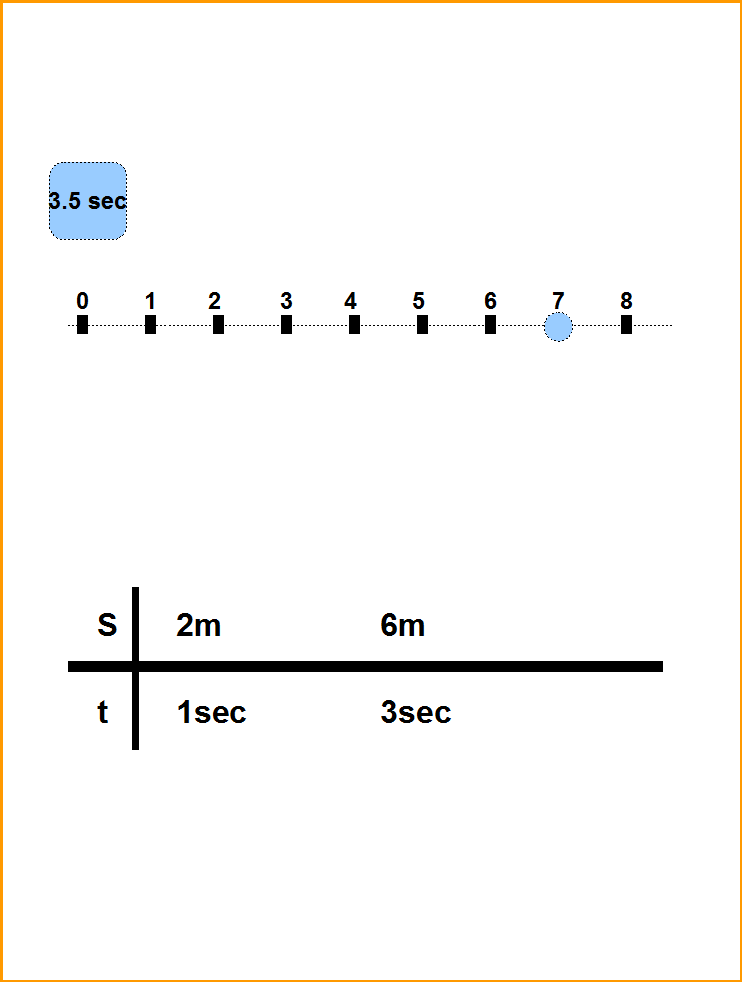
Рис.6. Равномерное движение точки по прямой линии. Результаты измерений приведены в виде таблицы, в которой данные расположены горизонтально, а взаимосвязанные пары время- пройденное расстояние, вертикально.
Но тела не всегда не движутся с постоянной скоростью. Они или разгоняются сначала, или останавливаются после некоторого времени. В таких случаях говорят, что они ускоряются.
Если в момент времени t1 скорость тела была v1, а в момент времени t2 скорость стала равна v2, то ускорение а вычисляется с помощью следующего преобразования:
а = (v2-v1)/(t2-t1).
Словами это можно сказать так: ускорение- это изменение скорости за промежуток времени делённое на этот промежуток времени. Изменение скорости- это v2-v1. Промежуток времени- это t2-t1.
Как видим преобразования которые дают нам скорость и ускорение похожи. Только в случае скорости, область определения- это длины пройденного пути, и область значений - скорости. А в случае ускорения область определения- скорости, а область значений - ускорения. Но в обоих случаях само преобразование- это изменение величин из области определения деленное на соответствующий интервал времени, в течении которого величины изменялись.
С точки зрения математики, эти преобразования аналогичны. Такое преобразование называется "вычисление производной" или просто "производная". Например, "производная пройденного пути по времени" или "производная скорости по времени". Но с точки зрения физики они существенно отличаются. И их отличие в размерности, т. е. в том, в чем измеряются скорость и ускорение. Дело в том что в математике, все числа и точки не имеют ни веса, ни длины, ни температуры. Все же физические величины состоят из двух частей. Первая часть- это число, которое характеризует насколько велика эта величина. Это её размер. А вторая часть указывает в чем данная величина измеряется. Например в метрах, или в сантиметрах, в килограммах, или в градусах. Это часть характеризует размерность физической величины. Поскольку пройденный путь измеряется в нашем случае в метрах, а время в секундах, то скорость будет измеряться в метрах деленных на секунду: м/сек. Но раз скорость измеряется в метрах деленных на секунду, а промежуток времени по прежнему измеряется в секундах, то размерность ускорения будет уже (м/сек)/сек= м/сек2 .
Например, за 4 секунды машина набрала скорость 20 м/сек. Значит при таком разгоне она в среднем набирала
(20 м/сек) /4 сек = 5 м/(сек за одну сек) или 5м/(сек*сек).
В конце Занятия есть Приложение, которое более подробно объясняет, что такое размерность.
В занятии Занятие 2, вторая неделя по программе второго года обучения мы подробно разбирали свойство инерции тел. Наши опыты показали, что инерционность тел определяется их массой. Чем тяжелее тело, тем медленнее оно ускоряется. Рисунок 7 показывает один из случаев представленных на видео https://www.youtube.com/watch?v=D8EeqbV6-Xw&feature=youtu.be . Рисунок объясняет, как измеряется скорость и ускорение в этом случае.
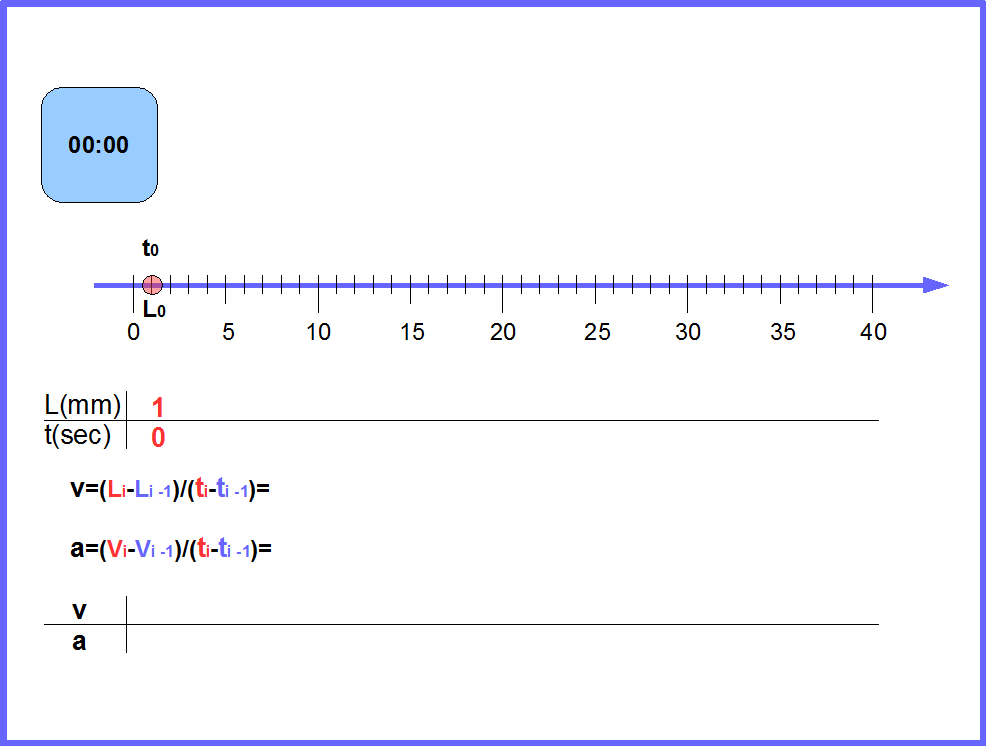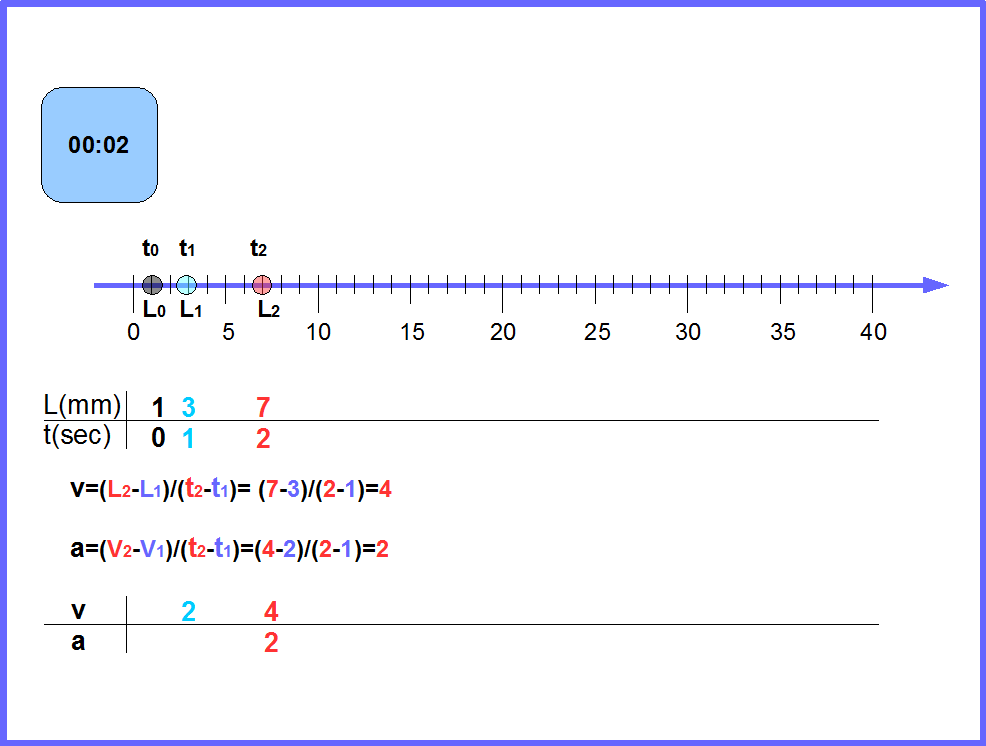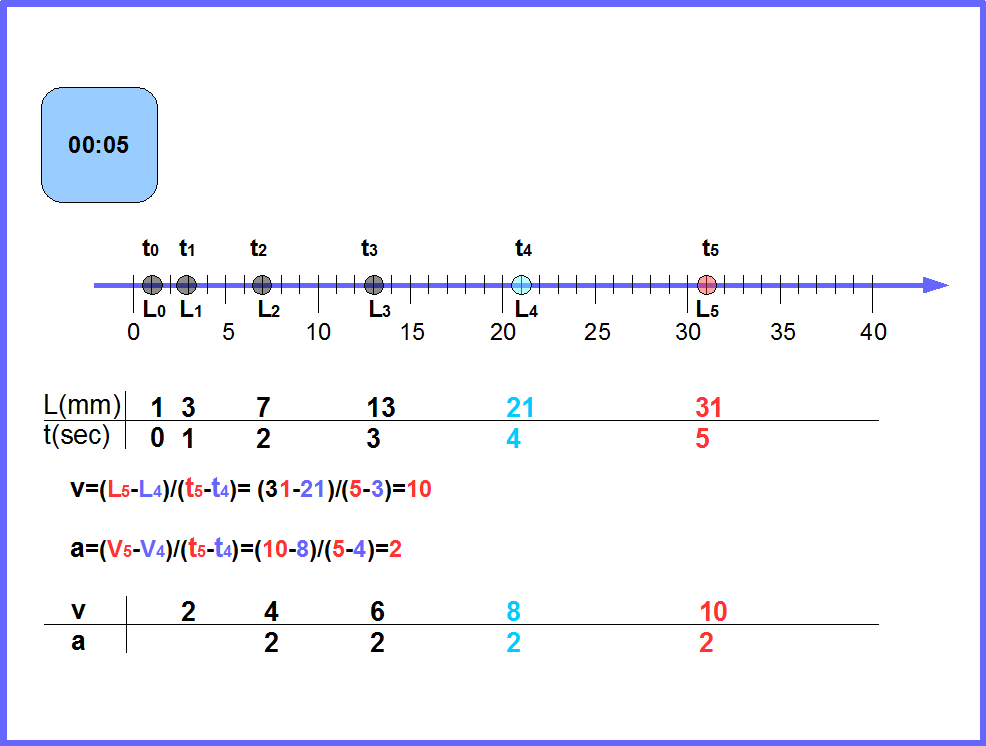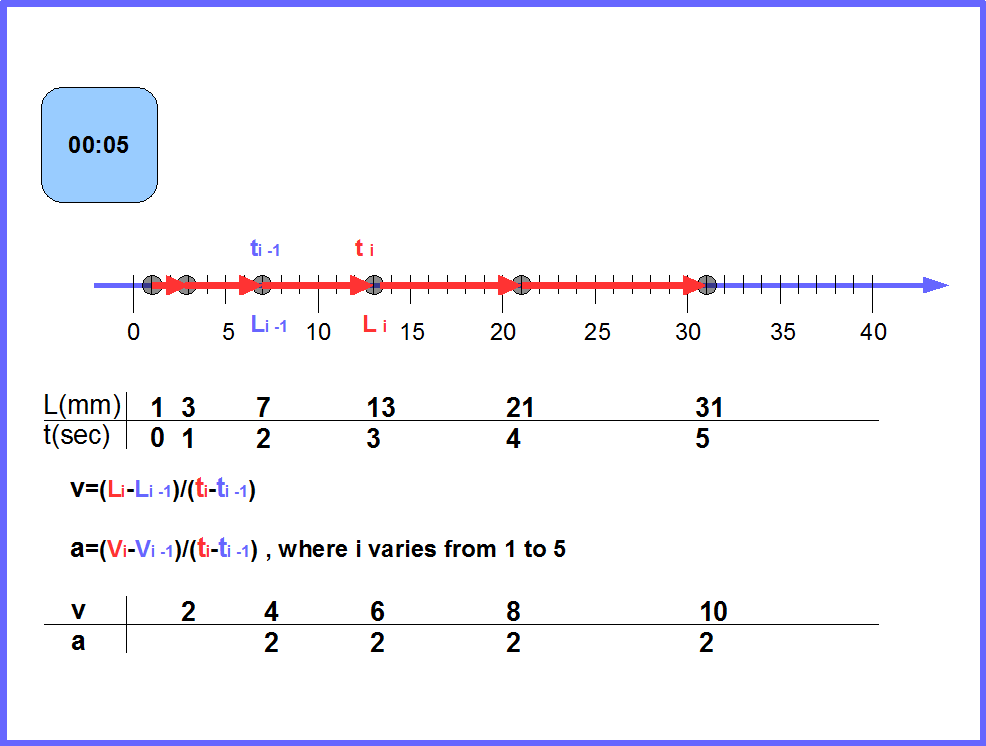
Рис.7. Рисунок схематично показывает равноускоренное движение тележки по прямой. Постройте по приведенным данным графики скорости и ускорения от времени.
Чтобы тело ускорялось на него должна действовать какая нибудь сила. Иначе тело будет или всегда покоиться, или двигаться прямолинейно и равномерно. Мы знаем, что если мы хотим увеличить ускорение a , то надо или прикладывать еще большую силу или уменьшать массу тела. Т.е. ускорение прямо пропорционально силе F, с которой мы действуем на тело, и обратно пропорционально массе тела m. Эти два утверждения можно записать математически как
a= F/m .
Отсюда получаем
F= m*a .
Как вы уже знаете, это уравнение называется Вторым Законом Ньютона. Сила это физическая величина, и как всякая физическая величина имеет размерность. Ее можно определить из формулы Ньютона. Она равна (масса*длина)/(время*время), или в единицах системы SI, это запишется как кг*м/сек2. Единичная величина 1 кг*м/сек2 называется единицей силы в системе SI, и в честь Исаака Ньютона, она называется Ньютоном. Сокращенно единица силы записывается как 1N , или 1Н если на русском языке. Величина 1 кг*м/сек2 равна силе действующей на тело массой 1 кг и сообщающую ему ускорение равное 1 м/сек2 .
Еще мы знаем, что если тело положить на опору (например, на пленку, фольгу, пластину, лист или дощечку) или подвесить на подвесе (например, на веревке, проволоке, резинке или пружине), то тело будет действовать на эту опору или подвес с силой равной весу тела. Эта сила создается гравитационной силой притяжения Земли. Как и всякая другая сила действующая на тело, гравитационная сила притяжения Земли способна ускорять тело согласно закону Ньютона.
В видео https://www.youtube.com/watch?v=8UbQglH5EUM исследуется ускорение создаваемое силой притяжения Земли. Для этого взяты два грузила с разным весом. Одно из них свинцовое, другое деревянное. Сначала они взвешиваются разными способами, чтобы показать, что их вес и массы действительно разные. Затем они подвешиваются и одновременно отпускаются. Замедленная съемка показывает, что они начинают падать и достигают поверхности стола одновременно несмотря на разницу их масс. Поэтому, если посчитать их ускорения, то они окажутся одинаковыми. Значит сила притяжения P (или её еще называют сила тяжести) действующая на тело массой m придает ему ускорение равное g, и это ускорение одинаково для всех тел на поверхности Земли. Это ускорение g называется ускорением свободного падения. Оно равно g=9.8м/сек2. .А силу притяжения P тогда можно записать в виде:
P= m*g
Рассмотрим, к каким последствиям может приводить действие силы тяжести на опору. Очевидно, что всякая опора начинает хотя бы немного, но прогибаться. Или говорят, опора деформируется. Жесткие опоры деформируются меньше, мягкие и эластичные- больше. Остановимся на «мягких» опорах. В качестве примера возьмем снег и человека идущего по снегу. Если снег глубокий и рыхлый, то человек провалится. Чтобы не проваливаться, люди придумали снегоступы. Почему в снегоступах человек может ходить по рыхлому снегу и не проваливаться, ведь вес человека не меняется? Оказывается важна не только сила тяжести, но площадь опоры. Чем больше площадь опоры, тем меньше будет проседать снег. С другой стороны, очевидно, что величина проседания снега (обозначим её через η) прямо пропорциональна весу человека. Поэтому для величины проседания можно записать:
η=k*P/A
, где А- площадь опоры, Р- сила тяжести действующая на человека, или его вес, k- некоторая константа, которую мы пока не знаем. Это уравнение показывает важность величины Р/А. Величина Р/А называется давлением. Поскольку она равна силе деленной на площадь, то её размерность будет (масса*длина)/(время*время*длина*длина)= масса/(время*время*длина), но обычно единицу измерения пишут в виде сила/площадь. Например, Ньютон деленный на метр в квадрате, Н/м2.
ДОМАШНИЕ ЗАДАНИЯ.
С помощью OpenOffice Presentations (для тех кто забыл, здесь можно прочесть, как пользоваться OpenOffice для создания gif файлов : "Делаем мультфильм"), сделайте следующие мультфильмы-gif файлы:
1. Мультфильм равномерное и равноускоренное/равнозамеделенное движение:
2. Шагающие на месте ноги:

3. Идущие ноги:

4. Шагающий на месте человечек (ноги и руки- это толстые отрезки аналогичные тем, что вы рисовали в садачах 2 и 3):

5. Идущий человечек:

ПРИЛОЖЕНИЕ
При подсчете скоростей и промежутков времени, мы используем размерности. Размерность любой физической величины- это то физическое свойство, которое эта величина характеризует. Например, у расстояния размерность длина, у времени- время. Существуют основные размерности: длина, масса, время. Мы также отнесем к ним и температуру. Кроме них есть физические величины, чьи размерности получаются из основных.
Например, найдем размерность площади плоской фигуры. Независимо от того, возьмем мы большую фигуру или самый маленький квадрат, или мы сложим/объединим две плоские фигуры, их размерность должна быть одной и той же. И она должна характеризовать суть площади. Суть же площади состоит в том, что мы определяем, сколько квадратов с единичным размером может поместиться в данной плоской фигуре. Площадь квадрата равна произведению длин его сторон. Следовательно, его размерность должна быть длина в квадрате: LxL или L2. Но тогда размерность любой другой фигуры должна быть тоже L2, поскольку её площадь получается сложением площадей маленьких квадратов, а размерность при сложении фигур не меняется.
К величинам, чьи размерности получаются из основных, относятся также скорость и ускорение. Скорость- это расстояние пройденное за единицу времени. Чтобы её найти, надо расстояние, пройденное за время t, поделить на это время. Поэтому её размерность- длина деленная на время: L/t.
Физические свойства величин характеризуются с помощью размерностей. Но для того, чтобы измерить величины и вычислять их значения нужны конкретные единицы измерения. Существует огромное количество самых разных физических величин. Возникает вопрос- какие единицы измерения надо использовать для них? Что, для каждой новой физической величины надо придумывать свою единицу измерения? А это значит надо создавать новый стандарт для каждой новой единицы измерения. Хранить его, изготавливать и рассылать всем его копии. К счастью, размерность и единицы измерения любой физической величины взаимосвязаны. Единица измерения физической величины всего лишь запись размерности величины с использованием выбранных единиц измерения. Зная единицы измерения размерностей основных величин и размерность самой величины, не сложно вычислить её единицы измерения.
Например, размерность скорости длина деленная на время (L/t). Соответственно, единицей измерения скорости можно взять км/час, см/сек, км/см и так далее.
Поэтому можно ограничиться стандартами мер только для основных размерностей : длины, массы, времени, градуса. Ведь остальные размерности можно вывести из них. Но для этого надо уметь вычислять размерности физических величин. А для этого должна существовать теория описывающая свойства этих физических величин. Т.е. размерность физических величин и физические законы тоже взаимосвязаны.
Самое удивительное в этом то, что требуется знание только нескольких основных физических свойств, чтобы описать все известные нам явления. Например, свойство тел при нагреве менять свои размеры характеризуется размерностью длина деленная на температуру : L/T. Поэтому достаточно замерить изменение размеров тела при изменении температуры. Обычно при небольшом изменении температур, график этой зависимости близок к прямой линии, и зависимость называется линейной (помните, мы с вами проходили такие преобразования). Иначе говоря длина тела меняется пропорционально изменению его температуры. В таком случае расширение тел описывается линейным уравнением с постоянным коэффициентом теплового расширения (он является коэффициентом пропорциональности), с размерностью L/T. Для большинства известных материалов такие коэффициенты измерены и их можно найти в справочниках.
Посмотрим , как вычисляется ускорение. Расстояние измеряется в километрах, метрах, сантиметрах, миллиметрах и так далее. Допустим мы выбрали сантиметры. Следовательно размерность расстояния, длина, у нас будет записываться в сантиметрах. Время может измеряться в часах, минутах, секундах. Пусть мы стали использовать секунды. Тогда размерность скорости, длина/время, в нашем случае запишем, как сантиметр в секунду: см/сек. Например, наблюдаемая тележка в начальный момент времени t1=0 sec имела скорость 0 см/сек. Предположим она ускорилась до скорости v2= 6см/сек к моменту времени t2= 2 сек. Значит её ускорение было a= (v2-v1)/(t2-t1)= (6см/сек-0см/сек)/(2сек-0сек)= 6 см/сек / 2 см/сек = 6/2 см/(сек*сек)= 3 см/(сек*сек). Произведение сек*сек это секунда в квадрате: сек2. Соответственно ускорение можно записать так: а= 3 см/сек2, или используя обозначения Basic, a = 3 см/сек^2.
Как мы уже много раз говорили, запись физической величины всегда состоит из двух частей. Первая- это число. Вторая- размерность, точнее единица измерения представляющая размерность этой физической величины. Единицами измерения могут быть километры, метры, секунды, градусы и т.д.. Условно, физические величины можно представлять, как произведение числа на размерность, а конкретнее, числа на единицу измерения размерности. Но знак умножения при этом умалчивается. Поэтому когда мы делим одну физическую величину на другую, то мы делим не только числа, а всё произведение числа на размерность на другое число, и на его размерность. Аналогично при произведении физических чисел перемножаются сами числа и их размерности. При сложении или вычитании двух физических величин, их размерности должны быть одинаковыми. Ведь мы можем складывать и вычитать яблоки только из яблок, но не яблоки из апельсин. Согласно правилу дистрибутивного умножения, размерность можно вынести за скобку. Например, машина проехала сначала 10 км, а затем ещё 3 км. Полный пройденный путь равен 10км +3км = (10+3)км= 13км.
Поскольку размерность в каждом конкретном измерении записывается с помощью единиц измерения, часто эти понятия не различают, но всегда помнят, что у одной и той же размерности может быть много разных единиц измерения. Например у размерности «длина» единицами измерения могут быть километры, метры, сантиметры, миллиметры, микрометры или микроны, нанометры., Ангстремы. И поэтому, когда говорят или пишут, что размерность величины равна сантиметру, подразумевается, что на самом деле её размерность- длина.